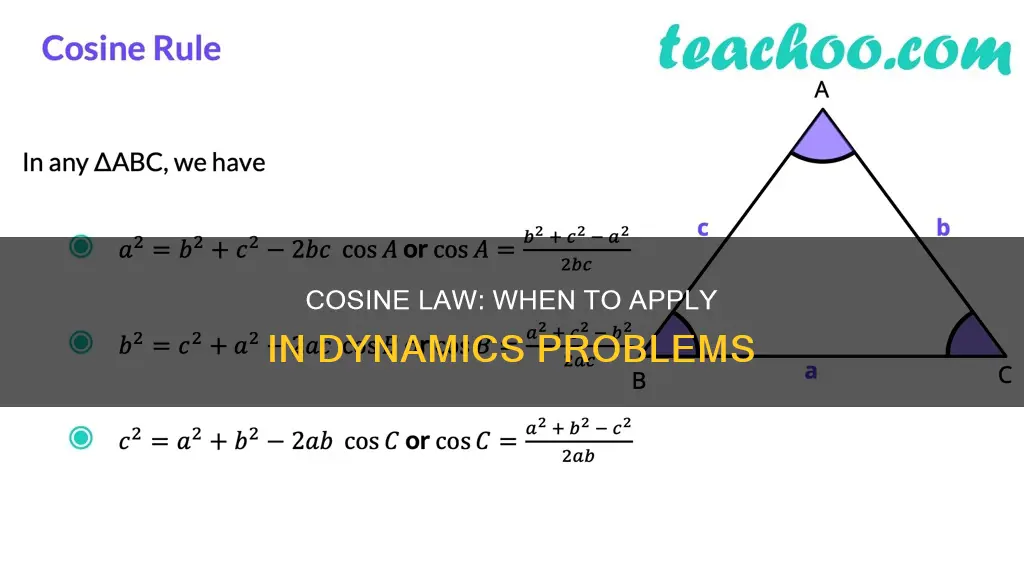
The Law of Cosines, also known as the Cosine Rule or Cosine Formula, is a trigonometric principle that relates the lengths of a triangle's sides to the cosine of one of its angles. It is used to determine the length of the third side of a triangle when the lengths of the other two sides and the angle between them are known. The formula for the Law of Cosines is c^2 = a^2 + b^2 - 2ab cos(C), where a, b, and c are the sides of the triangle, and C is the angle between sides a and b. This law can be applied to any triangle, not just right triangles, and is useful when solving dynamics problems involving triangles where the lengths of two sides and the included angle or the lengths of all three sides are known.
| Characteristics | Values |
|---|---|
| When to apply the Law of Cosines | When you have two sides and the included angle (SAS) or three sides (SSS) |
| What the Law of Cosines signifies | The relation between the lengths of sides of a triangle with respect to the cosine of its angle |
| When to use the Law of Cosines formula | When you have two sides and one angle or three sides of a triangle |
| When to use the Law of Sines | When you have two angles and a side (AAS or ASA) or two sides and a non-included angle (SSA) |
What You'll Learn

Using the Law of Cosines to find the unknown side of a triangle
The Law of Cosines, also known as the Cosine Rule or Cosine Formula, is a trigonometric principle that relates the lengths of a triangle's sides to the cosine of one of its angles. It is used to determine the length of the third side of a triangle when the lengths of the other two sides and the angle between them are known.
The Law of Cosines is expressed by the formula:
A^2 = b^2 + c^2 - 2bc * cos(α)
Where a, b, and c are the sides of the triangle, and α is the angle between sides b and c.
To use the Law of Cosines to find the unknown side of a triangle, follow these steps:
- Identify the known values: You should know the lengths of two sides of the triangle and the angle between them. Label the known sides as 'b' and 'c', and the unknown side as 'a'.
- Apply the Law of Cosines formula: Use the formula a^2 = b^2 + c^2 - 2bc * cos(α) to set up an equation. Make sure to substitute the known values into the formula.
- Simplify the equation: Simplify the equation by performing the multiplication and exponentiation operations.
- Solve for 'a': To solve for the unknown side 'a', take the square root of both sides of the equation. This will give you the length of the unknown side.
- Interpret the result: The value you obtain for 'a' represents the length of the unknown side of the triangle.
For example, let's say we have a triangle with sides a, b, and c, where b = 5 units, c = 8 units, and the angle between b and c is 60 degrees. To find the length of side a, we can apply the Law of Cosines:
A^2 = 5^2 + 8^2 - 2 * 5 * 8 * cos(60 degrees)
Simplifying the equation, we get:
A^2 = 25 + 64 - 80
A^2 = 11
Taking the square root of both sides, we find:
A = ±√11 units
So, the length of the unknown side 'a' in this triangle is approximately 3.32 units (rounded to two decimal places).
The Law of Cosines is a valuable tool in trigonometry, enabling us to solve for unknown sides or angles in triangles, making it an essential concept in the study of geometry and related fields.
Sharia Law: Understanding Its Application and Origins
You may want to see also

Using the Law of Cosines to find the unknown angles of a triangle
The Law of Cosines is a formula that relates the three sides of a triangle to the cosine of one of its angles. It is also called the Cosine Rule.
The Law of Cosines is used when we know the lengths of two sides of a triangle and the angle between them, and we want to determine the length of the third side. This is known as Case I.
The formula for Case I is:
C^2 = a^2 + b^2 - 2ab x cos(C)
Where:
- C is the side we want to find
- A and b are the known sides
- C is the angle between the known sides
The Law of Cosines can also be used to find the measure of an angle when the three sides of a triangle are given. This is known as Case II.
To use the Law of Cosines to find an unknown angle:
- Identify c as the side across from the angle you are trying to find.
- Substitute the values into the Law of Cosines formula.
- Solve the equation for angle C.
For example, let's say we have a triangle with sides a = 3, b = 5, and c = 7, and we want to find the measure of angle C. Using the Law of Cosines formula, we can set up the equation:
7^2 = 3^2 + 5^2 - 2 x 3 x 5 x cos(C)
Simplifying the equation gives:
49 = 9 + 25 - 30cos(C)
Solving for cos(C) gives:
Cos(C) = (49 - 34)/(-30)
Cos(C) = 15/(-30)
Cos(C) = -0.5
Using a calculator to find the arccos of -0.5 will give us the value of angle C.
The Law of Cosines is not just restricted to right triangles; it can be used for all types of triangles where we need to find any unknown side or angle.
Copyright Law: Understanding Applicable Regulations and Rules
You may want to see also

Using the Law of Cosines to solve word problems
The Law of Cosines, also known as the Cosine Rule or Cosine Formula, is a formula that relates the lengths of the sides of a triangle to the cosine of one of its angles. It is used to determine the length of the third side of a triangle when the lengths of the other two sides and the angle between them are known. This can be applied to all types of triangles, not just right triangles.
The formula for the Law of Cosines is:
C^2 = a^2 + b^2 – 2ab cosγ
Where a, b and c are the sides of a triangle and γ is the angle between a and b.
Example 1: Finding the Distance Travelled by a Boat
A boat leaves port, travels 10 miles, turns 20 degrees, and travels another 8 miles. How far is the boat from the port?
Solution: The boat turned 20 degrees, so the obtuse angle of the non-right triangle is the supplementary angle, 180°-20° = 160°. Using the Law of Cosines:
X^2 = 8^2 + 10^2 – 2(8)(10)cos(160°)
X^2 = 314.35
X = √314.35
X ≈ 17.7 miles
The boat is approximately 17.7 miles from the port.
Example 2: Determining the Location of a Cell Phone
There are two cell phone towers 6000 feet apart along a straight highway, and a cell phone is north of the highway. Based on the signal delay, it is determined that the signal is 5050 feet from the first tower and 2420 feet from the second tower. Determine the position of the cell phone north and east of the first tower, and its distance from the highway.
Solution: Using the Law of Cosines, we can solve for the angle θ. Let a = 2420, b = 5050, and c = 6000.
A^2 = b^2 + c^2 – 2bc cos θ
2420)^2 = (5050)^2 + (6000)^2 – 2(5050)(6000)cos θ
Cos θ ≈ 0.9183
Θ ≈ cos^-1(0.9183)
Θ ≈ 23.3°
Using the angle θ = 23.3° and basic trigonometric identities, we can find the solutions:
X = 5050cos(23.3°)
X ≈ 4638.15 feet
Y = 5050sin(23.3°)
Y ≈ 1997.5 feet
The cell phone is approximately 4638 feet east and 1998 feet north of the first tower, and 1998 feet from the highway.
Example 3: Calculating the Length of a Tunnel
An engineering firm is bidding on a proposed tunnel through a mountain. Given that the two ends of the tunnel are 6000 feet apart along a straight path, and one end is 5050 feet below the mountain surface while the other end is 2420 feet below, find the length of the tunnel and the bid amount.
Solution: Using the Law of Cosines, we can calculate the length of the tunnel:
C^2 = a^2 + b^2 – 2ab cos θ
C^2 = (5050)^2 + (2420)^2 – 2(5050)(2420)cos θ
C^2 ≈ 36,034,090
C ≈ √36,034,090
C ≈ 6000 feet
The length of the tunnel is approximately 6000 feet.
Example 4: Determining the Range of a Transmission Tower
A transmission tower is located 5000 feet due north of a communication centre. A receiver is located 3000 feet due east of the communication centre. The tower has a line of sight range of 7000 feet. Is the receiver within the range of the tower?
Solution: Using the Law of Cosines, we can calculate the distance between the tower and the receiver:
C^2 = a^2 + b^2 – 2ab cos θ
C^2 = (5000)^2 + (3000)^2 – 2(5000)(3000)cos(90°)
C^2 = 25,000,000 + 9,000,000 – 2(5000)(3000)(0)
C^2 = 34,000,000
C ≈ √34,000,000
C ≈ 5,831 feet
The distance between the tower and the receiver is approximately 5831 feet, which is within the range of the tower.
In summary, the Law of Cosines is a valuable tool for solving word problems involving triangles, particularly when dealing with non-right triangles and unknown side lengths or angles.
Antitrust Laws: When Do They Apply?
You may want to see also

Using the Law of Cosines to find the length across a lake
The Law of Cosines is a formula that relates the three sides of a triangle to the cosine of a given angle. It is also known as the Cosine Rule or Cosine Formula. This rule is used to find the length of the third side of a triangle when the length of the other two sides and the angle between them are known.
The Law of Cosines can be applied to find the length across a lake by treating the lake as one side of a triangle and the other two sides as the distance from one endpoint of the lake to the midpoint of the lake, and the distance from the other endpoint of the lake to the midpoint. By measuring the distances from each endpoint to the midpoint and the angle between them, you can use the Law of Cosines to calculate the length across the lake.
A^2 = b^2 + c^2 – 2bc * cos(α)
Where:
- A, b, and c are the sides of the triangle
- Α is the angle between sides b and c
For example, let's say you have a lake and you measure the following:
- Distance from endpoint A to the midpoint of the lake is 500 feet
- Distance from endpoint B to the midpoint of the lake is 300 feet
- The angle between these two distances is 60 degrees
Using the Law of Cosines formula, you can calculate the length across the lake (side a) as follows:
A^2 = 500^2 + 300^2 – 2(500)(300) * cos(60)
A^2 = 250,000 + 90,000 – 2(500)(300) * 0.5
A^2 = 340,000 – 300,000
A^2 = 40,000
A = 200 feet
So, the length across the lake is 200 feet.
This is a practical application of the Law of Cosines, and it helps students understand how this trigonometric law can be used in real-world scenarios.
Charles' Law: Liquids and Their Compressibility
You may want to see also

Using the Law of Cosines to find the distance a plane has travelled
The Law of Cosines is a formula that relates the three sides of a triangle to the cosine of one of its angles. It can be used to determine the length of the third side of a triangle when the lengths of the other two sides and the angle between them are known. This can be applied to any type of triangle, not just right triangles.
The formula for the Law of Cosines is:
A^2 = b^2 + c^2 – 2bc x cos(α)
Where a, b, and c are the sides of the triangle, and α is the angle between sides b and c.
To find the distance a plane has travelled using the Law of Cosines, we can apply this formula. Let's say we have two planes that take off from the same airport, and we want to find the distance between them after a certain amount of time. We can use the Law of Cosines formula, where the two sides of the triangle are the distances travelled by each plane, and the angle between them is the angle of their flight paths.
For example, if one plane has travelled 300 miles and the other has travelled 200 miles, and the angle between their flight paths is 40 degrees, we can calculate the distance between them using the Law of Cosines as follows:
C^2 = 300^2 + 200^2 – 2 • 300 • 200 • cos(40)
Taking the square root of the result gives us the distance between the two planes, which is approximately 423 miles.
So, the Law of Cosines can be applied to dynamics problems involving distances travelled by objects, such as planes, by treating the problem as a triangle and using the distances and angles involved to calculate unknown values.
Thermodynamics Law and the Carnot Cycle: Efficiency Explained
You may want to see also
Frequently asked questions
The law of cosines should be applied when you are working with a non-right-angled triangle and need to determine the length of the third side when the lengths of the other two sides and the angle between them are known.
The formula for the law of cosines is:
c^2 = a^2 + b^2 – 2ab cos C
where a, b and c are the sides of a triangle and C is the angle between sides a and b.
The law of cosines is used to solve triangles when given two sides and an included angle (SAS) or three sides (SSS). It can be used to find unknown sides and angles.







