Who Extended Ohm's Law To Ac Circuits?

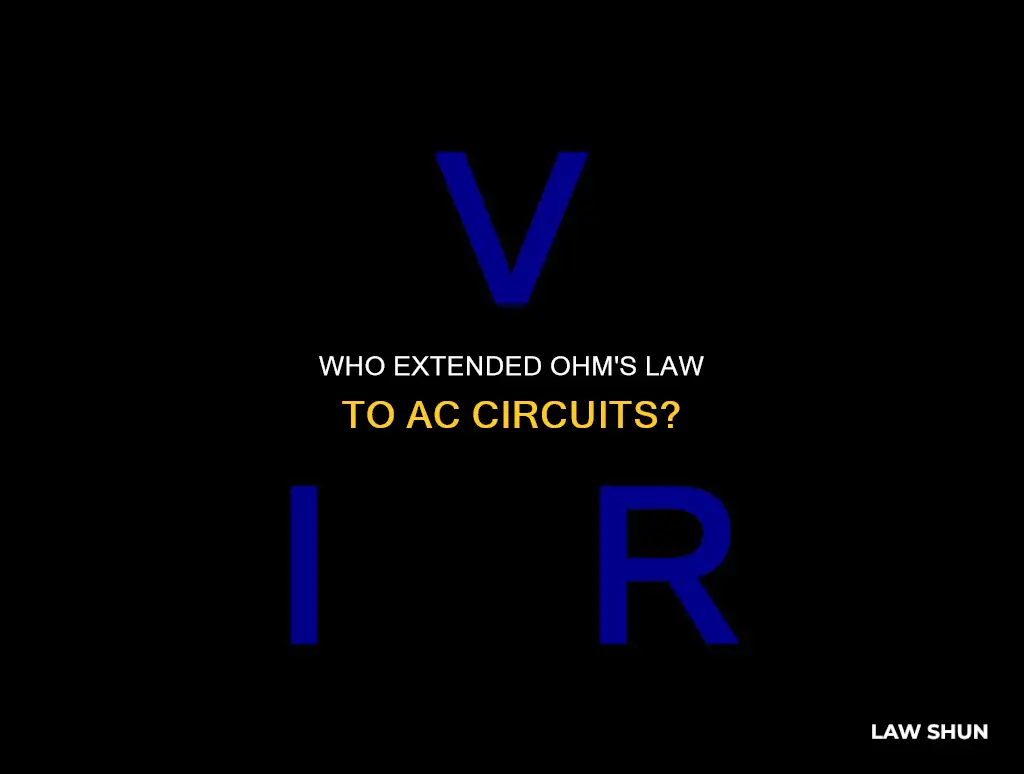
Georg Ohm's law, which states that the electric current through a conductor between two points is directly proportional to the voltage across the two points, is valid for AC circuits. However, AC circuits involve complex sources and impedances that vary with time or frequency, so the variables in the equation are not always real numbers. In AC circuits, the law must be modified to account for inductors and capacitors, which have different behaviours relative to resistors.

Impedance is the opposition in AC circuits that accounts for resistance and reactance

Impedance is a concept that expands on Ohm's Law to account for opposition in AC circuits, which is a combination of resistance and reactance.

Ohm's Law states that the electric current through a conductor between two points is directly proportional to the voltage across the two points. This can be expressed mathematically as:

V = IR or I = V/R or R = V/I

Where:

• V is the voltage measured across the conductor
• I is the current through the conductor
• R is the resistance of the conductor

In an AC circuit, however, the opposition to current flow is not just resistance but also reactance, and this combination is called impedance. Impedance is denoted by the letter "Z" and is measured in Ohms, just like resistance.

The formula for impedance in an AC circuit is:

Z^2 = R^2 + X^2

Or:

Z = sqrt(R^2 + X^2)

Where:

• Z is the impedance
• R is the resistance
• X is the reactance

Impedance is the total opposition to the flow of alternating electrical current in an AC circuit. It is influenced by the circuit's current-limiting components, such as resistance (R), inductance (L), and capacitance (C).

While resistance remains constant in both DC and AC circuits, reactance can change with frequency. This means that impedance is also frequency-dependent and has a phase angle associated with it.

In an AC circuit, the phase angle of reactance, whether inductive or capacitive, is always 90 degrees out-of-phase with the resistive component. This means that the resistive and reactive values cannot be simply added together arithmetically to get the total impedance. Instead, they are combined using Pythagoras' theorem, resulting in a vector sum of the resistance and reactance vectors.

In summary, impedance is a key concept in AC circuits, representing the total opposition to current flow and accounting for both resistance and reactance. It is calculated using a combination of these two values and is essential for understanding and designing AC circuits.

AC circuits involve complex sources and impedances which vary with time or frequency

AC circuits are more complex than their DC counterparts, involving sources and impedances that vary with time or frequency. This complexity necessitates a modified version of Ohm's law, where V = IZ, with Z representing impedance.

Ohm's law, V = IR, remains valid in AC circuits, but it is important to recognise that R, or resistance, is not the sole factor influencing voltage and current in these circuits. Capacitors and inductors, commonly found in AC circuits, introduce reactance, which causes a time displacement between voltage and current. This reactance results in a phase difference, requiring the inclusion of a phase angle in the modified Ohm's law equation.

At high frequencies, such as radio frequencies, the magnetic effects become significant, and the skin effect comes into play. This phenomenon, where currents are predominantly found in the outer parts of conductors, must be considered when designing high-frequency circuits.

Additionally, parasitic capacitance in resistors can subtly alter the phase relationship between voltage and current at high frequencies, causing the resistor to resemble a capacitor. Inductive reactance, another factor in AC circuits, further complicates the application of Ohm's law in these dynamic systems.

In conclusion, while Ohm's law can be applied to AC circuits, it is crucial to acknowledge the presence of complex sources and impedances that vary with time and frequency, necessitating a more nuanced understanding and application of electrical principles.

Capacitors and inductors have a different behaviour relative to resistors

Georg Ohm's law states that the electric current through a conductor between two points is directly proportional to the voltage across the two points. This empirical law was formulated in 1827 and is expressed by the equation:

V = IR or I = V/R or R = V/I

Where:

• I is the current through the conductor
• V is the voltage measured across the conductor
• R is the resistance of the conductor

Ohm's law applies to circuits containing only resistive elements (no capacitances or inductances) for all forms of driving voltage or current, whether direct current (DC) or time-varying alternating current (AC).

Capacitors, inductors, and resistors are all passive components used in electrical circuits. Passive means their behaviour changes little with voltage or current fluctuations. They differ from active components, such as diodes and transistors, which have a non-linear reaction to voltage and current.

Resistors impede the passage of electric current in a circuit and are designed to have a specific resistance value. They convert energy to heat and dissipate it. Resistors are used to restrict current flow and develop a voltage drop.

Capacitors and inductors, on the other hand, store energy in electric and magnetic fields, respectively. They impede the flow of electrons in a circuit but, unlike resistors, do not dissipate energy.

Capacitors store electric charge and oppose changes in voltage. They are commonly used in power supplies to remove high-voltage surges and smooth out voltage. They are also used in electric single-phase motors to help them start and develop full torque.

Inductors induce an electromagnetic field in the space around a conductor, storing energy that can later be returned as current. They oppose changes in current and are often used to smooth out current values, functioning as a 'choke'.

In summary, capacitors and inductors have a different behaviour relative to resistors. While resistors restrict current flow and dissipate energy as heat, capacitors and inductors store energy in electric and magnetic fields, respectively, and oppose changes in voltage and current.

The mathematics of AC circuits climb into complex domains

Georg Ohm's law, which states that the electric current through a conductor between two points is directly proportional to the voltage across the two points, is valid for AC circuits. However, AC circuits involve complex sources and impedances that vary with time or frequency. As a result, the mathematics of AC circuits climb into complex domains.

Ohm's law can be expressed as:

> V = IR

Where:

• V is the voltage measured across the conductor
• I is the current through the conductor
• R is the resistance of the conductor

In AC circuits, the relationship between voltage and current becomes the solution to a differential equation, so Ohm's law does not directly apply since it only contains resistance (R) and not complex impedances. These complex impedances may contain capacitance (C) or inductance (L).

The AC analogue to Ohm's law is:

> V = IZ

Where Z is the impedance of the circuit, and V and I are the rms or effective values of the voltage and current. The impedance Z is also the ratio of the voltage and current peaks, but the peaks of voltage and current do not occur simultaneously due to a phase angle associated with the impedance. This phase angle is necessary to characterise the circuit and calculate the average power used by the circuit.

In AC circuits, capacitors and inductors behave differently compared to DC circuits. The relationship between voltage and current for capacitors and inductors is more complex:

> V = L * dI/dt

> V = Initial value + (1/C) * Integral(I(t)dt)

Where:

• L is the inductance
• C is the capacitance
• T is time

The above equations show that the analysis of AC circuits involves calculus and differential equations, climbing into complex mathematical domains.

In summary, while Ohm's law is valid for AC circuits, the presence of complex impedances, capacitors, and inductors results in more intricate mathematics that climb into complex domains.

The current density in wires can be assumed to be constant across the cross-section of a wire for low frequencies

The current density in a wire refers to the amount of electric charge that flows through a chosen cross-sectional area per unit time. It is an important parameter in the design of electrical and electronic systems, as it determines the performance of a circuit.

In the case of low-frequency currents, such as those used in household electricity (60Hz), the current density can be assumed to be constant across the cross-section of a wire. This means that the electric charge is evenly distributed within the wire as it flows.

However, as the frequency of the current increases, the current density near the surface of the conductor becomes larger, while it decreases exponentially at greater depths. This phenomenon is known as the "skin effect". At high frequencies, such as radio frequencies, the magnetic effects become significant, and the currents are predominantly found in the outer parts of the conductor.

The skin effect has important implications for the design of high-frequency circuits. It reduces the effective cross-sectional area of the conductor, leading to an increase in resistance. This, in turn, can result in undesirable consequences, such as the conductor melting or burning up, or changes in the desired electrical properties.

To mitigate the skin effect, specialised multistrand wires like litz wire can be used. Litz wire consists of multiple insulated strands woven together, ensuring that the current is evenly distributed among them, thus reducing the overall increase in resistance.

Frequently asked questions