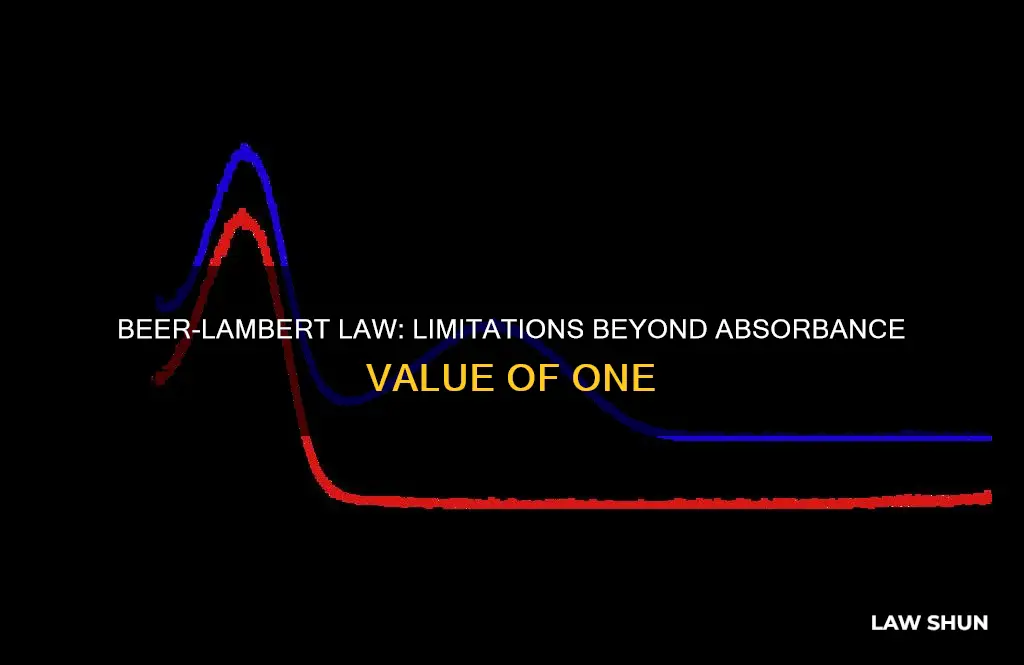
Beer's law, also known as the Beer-Lambert law, is a fundamental concept in absorption spectroscopy. It states that the concentration of a chemical solution is directly proportional to the absorbance of light that passes through it. However, this law has limitations and tends to break down at very high concentrations, especially above an absorbance of 1. At such high concentrations, the absorbance is no longer a good measure of the concentration, as all the light passing through the solution may be absorbed, and the relationship between absorbance and concentration becomes nonlinear. Additionally, at very low concentrations, the difference in light intensity before and after it passes through the solution becomes so small that it is difficult to measure accurately. Therefore, Beer's law is most effective at moderate concentrations, where the absorbance remains below 1.
| Characteristics | Values |
|---|---|
| Fundamental Limitations | |
| Absorbance above 1 | All light is absorbed |
| High concentrations | Analyte molecules are no longer independent of each other |
| High concentrations | Analyte's absorptivity depends on the solution's refractive index |
| Low concentrations | Amount of radiation absorbed is undetectable |
| Low concentrations | Measurements have too much error |
| Chemical Limitations | |
| Analyte is involved in an equilibrium reaction | |
| Instrumental Limitations | |
| Stray radiation | Light reaches the detector without passing through the sample |
| Non-monochromatic radiation | Passed radiation has a small but finite effective bandwidth |
What You'll Learn
- The law assumes no interaction between analyte molecules, which may not hold at high concentrations
- The analyte's absorptivity depends on the solution's refractive index, which varies with concentration
- The law assumes purely monochromatic radiation, but real-world radiation has a small but finite effective bandwidth
- Stray radiation can enter the instrument and reach the detector without passing through the sample
- At high concentrations, the analyte may undergo association, dissociation, or interaction with the solvent, producing a product with different absorption characteristics

The law assumes no interaction between analyte molecules, which may not hold at high concentrations
The Beer-Lambert law, commonly called Beer's law, states that the concentration of a chemical solution is directly proportional to the absorbance of a beam of light passing through it. However, this law assumes that the molecules of the analyte in the solution do not interact with each other. This assumption breaks down at high concentrations, where molecules are more likely to interact. Such interactions can be physical or chemical in nature.
Physical interactions between analyte molecules do not alter their polarizability as long as the interaction is not strong enough for light and molecular quantum states to intermix (a phenomenon known as strong coupling). However, they can cause attenuation cross-sections to become non-additive via electromagnetic coupling. On the other hand, chemical interactions can change the polarizability of the molecules, and thus their absorption.
In solutions, the assumption of no interaction between analyte molecules holds reasonably well since the molecules are far apart and do not scatter light at common analytical wavelengths (ultraviolet, visible, or infrared). However, at high concentrations, the molecules are closer together, and interactions can set in, leading to a negative deviation from Beer's law.
Illinois Ballot Initiatives: Becoming Law
You may want to see also

The analyte's absorptivity depends on the solution's refractive index, which varies with concentration
The refractive index of a substance is a fundamental constant that describes the interaction between light and matter. It is defined as the ratio of the speed of light in a vacuum to the speed of light in the substance. This change in speed causes light rays to bend, or refract, as they pass through the substance. The refractive index of a vacuum is 1, and for most other materials, it is greater than 1, meaning light travels slower in these substances than in a vacuum.
The refractive index of a substance is dependent on its composition and structure. It can vary with changes in temperature, wavelength of light, and concentration of solutes in a solution. For example, a higher temperature leads to a less dense substance, causing light to travel faster and resulting in a lower refractive index.
The refractive index is also related to the absorption of light in a substance. The absorption of light by a substance is described by the Beer-Lambert law, which states that the absorption of light is proportional to the concentration of the substance and the path length of light through the substance. The molar absorptivity, or extinction coefficient, of a substance is a measure of how well it absorbs light at a particular wavelength.
In summary, the refractive index of a substance is a fundamental constant that describes how light interacts with matter. It varies with the concentration of solutes in a solution, influencing the speed of light and the degree of light absorption. The absorption of light by a substance is described by the Beer-Lambert law, which takes into account the concentration of the substance and the path length of light. The analyte's absorptivity is dependent on the solution's refractive index, creating a relationship between concentration, refractive index, and absorption.
Inflation Reduction Act: Law and Its Impact
You may want to see also

The law assumes purely monochromatic radiation, but real-world radiation has a small but finite effective bandwidth
The Beer-Lambert law, also known as Beer's law, is an empirical relationship that describes the attenuation in intensity of a radiation beam as it passes through a medium. The law states that the intensity of radiation decreases exponentially with the concentration of the absorbing species in the medium. However, this law assumes that the radiation is purely monochromatic, meaning it consists of only a single wavelength. In reality, radiation often has a small but finite effective bandwidth, meaning it contains a range of wavelengths. This deviation from purely monochromatic radiation can lead to inaccuracies in the application of Beer's law.
Spectroscopic instruments typically use a device called a monochromator to select a specific wavelength of radiation to shine on a sample. A monochromator usually consists of a prism or other dispersing element and a slit, which work together to isolate a specific wavelength of radiation. However, it is important to note that even with a monochromator, it is challenging to obtain purely monochromatic radiation. The slit in the monochromator allows a "packet" of wavelengths through to the sample, with the packet centred on the desired wavelength. The width of this packet, known as the effective bandwidth, depends on the slit width and the ability of the dispersing element to separate different wavelengths.
Reducing the width of the slit can help achieve more monochromatic radiation by narrowing the packet of wavelengths that reach the sample. However, this also reduces the power of the radiation (Po) reaching the sample, which can increase the impact of background noise on the measurements. Therefore, there is a trade-off between achieving high monochromaticity and maintaining sufficient radiation power for accurate detection.
When polychromatic radiation is used, the total absorbance is no longer linear with concentration. Instead, a negative deviation occurs at higher concentrations due to the polychromicity of the radiation. This deviation becomes more pronounced when there is a larger difference in the molar absorptivity at different wavelengths. Therefore, it is preferable to perform absorbance measurements in a region of the spectrum where the absorption peak is relatively broad and flat, as this will result in less deviation from linearity.
Tax Reform: Lawmaking Process Explained
You may want to see also

Stray radiation can enter the instrument and reach the detector without passing through the sample
The expression for absorbance can be written as:
\[ \mathrm{A = \log\left(\frac{P_o}{P}\right)} \]
Where:
- \( \mathrm{A} \) = Absorbance
- \( \mathrm{P_o} \) = Power from the radiation source
- \( \mathrm{P} \) = Radiation reaching the detector after passing through the sample
Now, let's consider the presence of stray radiation (\( \mathrm{P_s} \)). The expression for absorbance, including this additional term, becomes:
\[ \mathrm{A = \log\left(\frac{P_o + P_s}{P + P_s}\right)} \]
At low concentrations, the amount of radiation absorbed by the sample (\( \mathrm{P} \)) is similar in magnitude to \( \mathrm{P_o} \). Even with the addition of \( \mathrm{P_s} \), the denominator (\( \mathrm{P + P_s} \)) remains relatively close to \( \mathrm{P_o} \). Thus, the effect of stray radiation on the absorbance measurement is negligible, and Beer's Law remains linear.
However, as the concentration of the sample increases, more radiation is absorbed, resulting in a decrease in \( \mathrm{P} \). At high concentrations, \( \mathrm{P} \) becomes much smaller than \( \mathrm{P_s} \). In this case, the denominator (\( \mathrm{P + P_s} \)) approaches the constant value of \( \mathrm{P_s} \), causing the absorbance to approach a constant value as well. This deviation from linearity at higher concentrations represents a negative deviation from Beer's Law.
Therefore, the presence of stray radiation can impact the accuracy of absorbance measurements, particularly at higher concentrations of the sample, leading to a breakdown of the linear relationship described by Beer's Law.
Trumpcare: Law or No-Go?
You may want to see also

At high concentrations, the analyte may undergo association, dissociation, or interaction with the solvent, producing a product with different absorption characteristics
Beer's Law, also known as the Beer-Lambert Law, is a law in physics that states that a beam of visible light passing through a chemical solution of fixed geometry will experience absorption proportional to the solute concentration.
However, Beer's Law is not always valid and has its limitations. One of the reasons for the deviation from Beer's Law is that at high concentrations, the analyte may undergo association, dissociation, or interaction with the solvent, producing a product with different absorption characteristics. This is known as a chemical deviation.
In detail, at high concentrations, the analyte molecules are more likely to interact with each other, and this assumption is used to derive Beer's Law. This effect leads to a negative deviation from Beer's Law. The interaction between analyte molecules can be divided into physical and chemical interactions. Physical interactions do not alter the polarizability of the molecules, as long as the interaction is not strong enough for light and molecular quantum states to intermix. On the other hand, chemical interactions can change the polarizability and, thus, absorption.
Additionally, Beer's Law assumes that the molecules absorbing radiation do not interact with each other. However, this assumption breaks down at high concentrations, as the molecules are closer together and can influence each other. This results in a deviation from the expected linear relationship between absorbance and concentration described by Beer's Law.
Furthermore, limitations of the Beer-Lambert Law include deviations in absorptivity coefficients at high concentrations due to electrostatic interactions between molecules in close proximity. This can lead to scattering of light and fluorescence or phosphorescence of the sample, causing a deviation from the ideal linear relationship predicted by Beer's Law.
Therefore, Beer's Law becomes ineffective at high concentrations due to the analyte undergoing various interactions and deviations from the assumptions made in the derivation of the law. These interactions and deviations result in a non-linear relationship between absorbance and concentration, contrary to what is predicted by Beer's Law.
The Legislative Process: How Bills Become Law
You may want to see also
Frequently asked questions
Beer's law assumes that the molecules of the absorbing substance do not interact with each other. However, at high concentrations, these molecules are more likely to interact, altering their ability to absorb radiation and resulting in a negative deviation from the law.
At low concentrations, the difference between the power of incident radiation, Po, and the power of transmitted radiation, P, becomes very small, leading to a high relative error in absorbance measurements. Additionally, the absorbance values are so low that they are difficult to distinguish from the background noise of the measuring instrument.
It is best to measure absorbance values within the range of 0.1 to 0.8. Absorbance values above 1 are generally undesirable as they introduce significant errors and reduce precision.